I’m an instrumentation and data collection geek. I love the challenge of developing ways to monitor the systems of my house and making sure they’re working properly. I’ve had a couple bad experiences where systems failed and not knowing it soon enough caused problems.
I have a solar tracker system, one which follows the sun when it’s up. It failed once with a hydraulic leak, and it was a couple days before I noticed it. Never again!
I’ve built and installed a monitoring system including its own solar panel, battery, 9 degree of freedom MEMS device normally used for inertial navigation of unmanned aerial vehicles, a microcontroller, and a LoRa radio with enough range to cover the distance to my house.
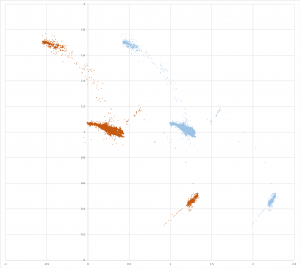
I’ll go into the details in another post. What I want to put into this post is the 3D plot of the first telemetry data.
The solar tracker is on a pillar out in my yard; the whole rotates around the vertical axis of the pillar (azimuth), and the panel tilts up and down (the motion is called nutation, the result is called elevation). The inertial navigation system (INS) device measures linear acceleration, angular acceleration, and magnetic field, all in 3D. My first task is to develop a coordinate system with one axis parallel to the axis of nutation of the solar tracker.
I have collected thousands of data points, taken at 1 minute intervals, and including the 3 linear accelerations. These mostly reflect the gravity vector. I’ve now plotted these in 3D; they should all lie in a plane, perpendicular to the axis of nutation. I can see this in the plot. (Look at the picture with 3D glasses, red filter for left eye, cyan filter for right eye.)
My next step is to calculate cross products for many pairs of vectors. The cross products will be perpendicular to each of the vectors, and so all the cross products should be collinear with each other, and also with the axis of nutation.
With 40,000 data points, there would be n(n-1) pairs, and hence 1.6 billion cross products. That’s a lot of computation. But I reckon that crossing vectors that are close together will yield poor results, and account for a lot of noise. So I’ll cross only those vectors that are farther apart, by some arbitrary distance.